Method
Microarray data is noisy gsnapshoth of transcriptional state of cells. Detecting biological correlations among gene expression profiles from multiple laboratories on a large scale remains difficult.
Here, we applied a module (sets of genes working in the same biological pathway)-based correlation analysis in combination with a network analysis to Arabidopsis data and developed a grelation map,h which represents relationships among DNA microarray experiments on a large scale. In each experiment, the gene expression responses of modules are closely correlated with the status of specific biological actions. Therefore, one can assume that samples sharing a common response in a module also share a related biological action or response. According to following idea, we chose modules from each experiment and calculated correlations between gene expression profiles by using it.
A. Dataset structure
Table 1 Example of data matrix of microarray data.
| Experiment A | Experiment B | Experiment C | ||||
| gene1 | a** | a* | a | |||
| gene2 | b | a | c | |||
| gene3 | c | c | f | |||
| gene4 | d | b | d | |||
*Characters (a, b, c, d..) in 'Table 1' indicate signal ratio of each gene, namely, log2 (average of signal intensity on treatment / average of signal intensity on control)
**Bold characters indicate genes contained in the module.
For a module, induced or repressed genes in each experiment were selected by statistical methods based on the P value of Studentfs t-test and the fold-change in induction levels between treatment and control samples. These genes represent the biological status of the samples analyzed in each experiment.
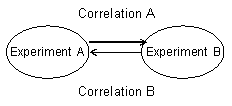
B. Calculation of correlation between experiments
Spearmanfs rank-order correlation coefficients (SCCs) to estimate relationships in gene expression profiles between experiments based on modules with bold characters.
Correlation A: From Experiment A to Experiment B
Experiment A (a, b, c) vs. Experiment B (a, a, c)
(Using a module of Experiment A)
Correlation B: From Experiment A to Experiment B
Experiment B (a, b) vs. Experiment A (b, d)
(Using a module of Experiment B)
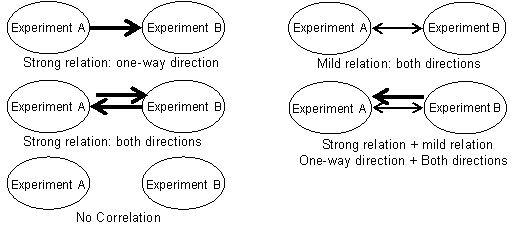
C: Drawing relation maps
Combining results based on SCC.